Model for rational numbers

Model for linear equation in one variable

Model for algebraic identities

Algebra model

Quadrilateral

Visit to mathematics resource center

Model of symmetry

Model of real number system

Methods of teaching

Question paper

Model of types of angles

Model of rotational symmetry

Model for real number system

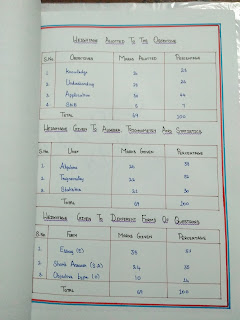
Frequency distribution

In statistics, a frequency distribution is a table or graph that displays the frequency of various outcomes in a sample.^[1] Each entry in the table contains the frequency or count of the occurrences of values within a particular group or interval, and in this way, the table summarizes the distribution of values in the sample.
frequency distribution shows us a summarized grouping of data divided into mutually exclusive classes and the number of occurrences in a class. It is a way of showing unorganized data e.g. to show results of an election, income of people for a certain region, sales of a product within a certain period, student loan amounts of graduates, etc. Some of the graphs that can be used with frequency distributions are histograms, line charts, bar charts and pie charts. Frequency distributions are used for both qualitative and quantitative data.

Construction of frequency distributionsEdit

1. Decide about the number of classes. Too many classes or too few classes might not reveal the basic shape of the data set, also it will be difficult to interpret such frequency distribution. The maximum number of classes may be determined by formula: ${\displaystyle \mathrm {NumberofClasses} =C=1+3.3\mathrm {log} (n)}$or ${\displaystyle C={\sqrt {n}}(\mathrm {approximately} )}$ where n is the total number of observations in the data.
2. Calculate the range of the data (Range = Max – Min) by finding minimum and maximum data value. Range will be used to determine the class interval or class width.
3. Decide about width of the class denote by h and obtained by ${\displaystyle h={\frac {\mathrm {Range} }{\mathrm {NumberofClasses} }}}$.

Generally the class interval or class width is the same for all classes. The classes all taken together must cover at least the distance from the lowest value (minimum) in the data set up to the highest (maximum) value. Also note that equal class intervals are preferred in frequency distribution, while unequal class interval may be necessary in certain situations to avoid a large number of empty, or almost empty classes.^[2]

1. Decide the individual class limits and select a suitable starting point of the first class which is arbitrary, it may be less than or equal to the minimum value. Usually it is started before the minimum value in such a way that the midpoint (the average of lower and upper class limits of the first class) is properly placed.
2. Take an observation and mark a vertical bar (|) for a class it belongs. A running tally is kept till the last observation.
3. Find the frequencies, relative frequency, cumulative frequency etc. as required.